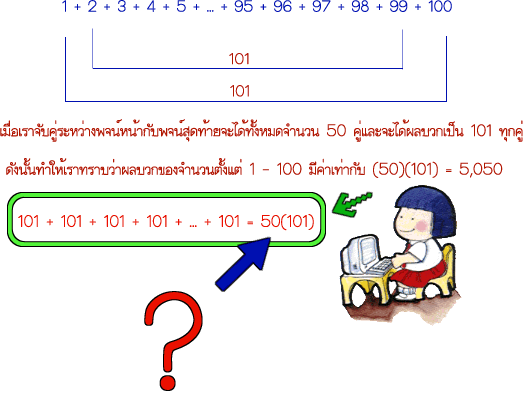
นักเรียนคงเคยหาผลบวกของจำนวนนับตั้งแต่ 1 ถึง 100 ซึ่งมีวิธีการหาที่หลากหลาย วิธีที่นักเรียนเคยทราบมาแล้วก็คือการใช้ทฤษฏีของ โยอันน์ คาร์ล ฟรีดริช เกาส์ ซึ่งได้คิดวิธีหา
ผลบวกของจำนวนซึ่งเป็นที่ยอมรับในปัจจุบัน นักเรียนลองศึกษาจากตัวอย่างข้างล่างนี้

ถ้าเราจะหาผลบวกของจำนวนตั้งแต่ 1 ถึง 1000 เราจะมีวิธีในการหาผลบวกของจำนวนดังกล่าวอย่างไร

จากปัญหาข้างต้นนักเรียนจะเห็นว่าถ้าจำนวนที่เราต้องการจะหาผลบวกนั้นมีจำนวนมากขึ้น เราก็จะต้องใช้เวลามากขึ้นตาม ดังนั้นเราจะหาวิธีใดสำหรับมาใช้หาอนุกรมโดยไม่ต้องเสียเวลามาก ซึ่งนักเรียนลองอาศัยการสังเกตจำนวนที่ได้ว่าแทนสิ่งใดในอนุกรม

จากสิ่งที่ได้เราสามารถสรุปได้ว่า ในการหาผลบวก n พจน์แรกของอนุกรมเลขคณิต

วีดิโอคลิปต่อไปนี้นักเรียนจะได้ศึกษาต่อเนื่อง หลังจากที่เราทราบแล้วว่าผลบวกของ n พจน์แรกของอนุกรมเลขคณิตหาได้จาก แต่สูตรดังกล่าวยังสามารถที่จะเปลี่ยนรูปเกิดเป็นอีกหนึ่งสูตร นักเรียนลองศึกษาจากวีดิโอคลิปต่อไปนี้