ลำดับอยู่ในรูปของการคูณ
|
|
| |
ลักษณะของลำดับที่อยู่ในรูปของการคูณ จะมีความแตกต่างจากลำดับที่เพิ่มค่าหรือลดค่าของลำดับ
นักเรียนลองสังเกตตัวอย่างข้างล่างนี้ แล้วพิจารณาดูความสัมพันธ์ที่เกิดขึ้นกับลำดับ
จากตัวอย่างดังต่อไปนี้
|
|
|
ตัวอย่างที่
1 จงหาพจน์ทั่วไปของลำดับ
2, 4, 8, 16, ...
|
| |
นักเรียนสังเกตเห็นอะไรในลำดับดังกล่าวหรือไม่ว่า
ลำดับชุดนี้ไม่ได้อยู่ในลักษณะของการเพิ่มค่าหรือลดค่าแต่อย่างใด ถ้าเราจะสังเกตต่อไปจะพบว่าพจน์ที่อยู่ถัดไปจะได้มาจากสองเท่าของพจน์ตัวหน้า
|
| |
|
| |
ตัวอย่างที่
2
จงหาพจน์ทั่วไปของลำดับ
10, 20, 40,
80, ...
|
| |
ตัวอย่างนี้ก็เช่นเดียวกันนักเรียนสังเกตเห็นว่าพจน์ที่อยู่ถัดไปจะได้มาจากสองเท่าของพจน์ตัวหน้า
แต่จะมีความแตกต่างจากตัวอย่างที่
1 นักเรียนจะทราบหรือไม่
ลองศึกษาดูรูปแบบโดยเลือก
|
|
|
|
จากทั้งสองตัวอย่างข้างต้น
นักเรียนลองทำแบบฝึกหัดต่อไปนี้
|
คำชี้แจง
ในการพิมพ์คำตอบกรณีเป็นกำลังให้ใช้สัญลักษณ์ " ^ " เศษส่วนใช้สัญลักษณ์
" / " และไม่ต้องเว้นวรรค เช่น n^2-3n-1 เป็นต้น
|
1. จงหาพจน์ทั่วไปของลำดับ
3, 9, 27, 81, ...
|
|
2. จงหาพจน์ทั่วไปของลำดับ
2, 6, 18, 54, ...
|
|
| |
ต่อไปจะเป็นลักษณะลำดับอีกลักษณะหนึ่งที่อยู่ในรูปของพหุคูณ ซึ่งนักเรียนก็คงเคยทราบมาแล้วที่เรามักจะคุ้นเคยกันก็คือ
"สูตรคูณ" นักเรียนลองศึกษาลำดับจากตัวอย่างต่อไปนี้
|
ตัวอย่าง
หาพจน์ทั่วไปของลำดับ
5, 10, 15,
20, 25, ...
|
| |
ขั้นที่ 1
ทำการสังเกตจากพจน์ที่ 1 ไปพจน์ที่ 2, ไปพจน์ที่ 3,
จะพบว่าทุกจำนวนของลำดับเป็นจำนวนที่เป็นพหุคูณของ
5
|
ขั้นที่ 2
สังเกตจำนวนที่คูณกับ 5 จะเป็นจำนวนเดียวกับลำดับที่ของพจน์
|
ขั้นที่ 3
เราจะพบแบบรูป (Pattern) ว่าพจน์ที่ n จะอยู่ในรูปของ 5 คูณกับลำดับที่ของพจน์
(ดังภาพที่แสดง)
|
| |
|
|
|
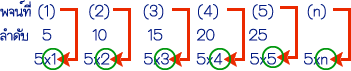
สรุปว่าพจน์ทั่วไปของลำดับ
5, 10, 15, 20, 25,
คือ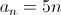 
|
|
| |
ตัวอย่าง
หาพจน์ทั่วไปของลำดับ
2, 4, 6, 8,
10, ...
|
| |
|
|
|
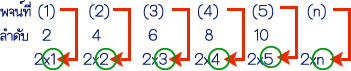
สรุปว่าพจน์ทั่วไปของลำดับ
2, 4, 6, 8, 10, ... คือ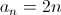 
|
|
| |
นักเรียนลองทบทวนลักษณะลำดับดังกล่าวข้างต้นจากแบบฝึกหัดต่อไปนี้
(พิมพ์ไม่ต้องใส่วงเล็บ เช่น 3n เป็นต้น)
|
1. จงหาพจน์ทั่วไปของลำดับ
7, 14, 21, 28, ...
|
2. จงหาพจน์ทั่วไปของลำดับ
10, 20, 30, 40, ...
|
|
| |
ต่อไปจะเป็นลักษณะของลำดับที่ค่อนข้างที่จะซับซ้อนเวลาที่เราจะมองหาพจน์ทั่วไป
ซึ่งเราจะต้องอาศัยความเข้าใจในรูปของพจน์ต่าง ๆ ที่ผ่านมา รวมไปถึงการสังเกตดูความสัมพันธ์ของพจน์ที่อยู่ถัดไปของลำดับมาเป็นส่วนประกอบในการพิจารณา
ดังตัวอย่างต่อไปนี้
|
ตัวอย่าง
จงหาพจน์ทั่วไปของลำดับ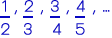 
|
|
เนื่องจากลำดับเป็นเศษส่วน
จึงทำการแยกพิจารณาโดยการพิจารณาลำดับของเศษ และลำดับของส่วน ดังภาพ
|
|
|
|
| |
สรุปว่าพจน์ทั่วไปของลำดับ
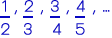คือ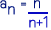 
|
|
| |
|
| |
ต่อไปเราจะลองมาศึกษาลักษณะลำดับที่อยู่ในรูปของพจน์กำลังสอง
ซึ่งอาจจะอยู่ในรูปของพหุนาม ในการหาพจน์ทั่วไปนั้นตามปกติก็จะเป็นเรื่องที่ยากที่เราจะหา
แต่นักเรียนลองศึกษา
ดูวีดิโอคลิปซึ่งจะอธิบายวิธีในการหารูปพจน์ทั่วไปแบบไม่ยาก ในตอนท้ายของคลิปจะเป็นลักษณะของการผสมผสานรูปแบบของพจน์ต่าง
ๆ ที่เราทราบ พร้อมกับมีตัวอย่างเพื่อตรวจสอบกฏเกณฑ์ต่าง ๆ และเมื่อศึกษาเสร็จเรียบร้อยแล้วให้เขียนสรุปสิ่งที่นักเรียนได้ศึกษา
พร้อมยกตัวอย่างประกอบลงใน 
|
| |
Quadratic
Pattern Finding the rule
|
ที่มา http://www.youtube.com/watch?v=qu__XCntcEU&feature=related
|
|
|
| |
จากวีดิโอคลิปข้างต้น
นักเรียนจะเห็นว่าการหาพจน์ทั่วไปของลำดับในรูปพหุนามกำลังสองจะไม่ใช่เรื่องยากอีกต่อไป
นักเรียนลองทำแบบฝึกหัดเพื่อทบทวนในสิ่งที่ศึกษา
|
คำชี้แจง
ให้นักเรียนพิมพ์ข้อความโดยไม่ต้องวรรค กรณีต้องยกกำลังให้ใช้สัญลักษณ์ ^
บนแป้นพิมพ์ เช่น n^2+3n-1 เป็นต้น
|
1. จงหาพจน์ทั่วไปของลำดับ
1, 3, 7, 13
|
2. จงหาพจน์ทั่วไปของลำดับ
2, 4, 8, 14, ...
|
|
ให้นักเรียนยกตัวอย่างลำดับที่อยู่ในรูปของพหุนามกำลังสองมาคนละ 1 ลำดับพร้อมแสดงวิธีการหาพจน์ทั่วไปในสมุดแบบฝึกหัด
|
|
|
| |
|
|
| |
| |
|
|
|
|
|
